
Zadanie Autostrada (aut)
Pomóż nam usprawnić bazę zadań!
Autostrada
Limit pamięci: 128 MB
Spółka AutoBajt zajmuje się budową jednej z autostrad w Bajtocji. Dotychczas firma pobierała opłaty przy wjeździe na autostradę, jednak nowy prezes, Bajtazar, zauważył, że w takiej sytuacji opłata nie zależała od liczby przejechanych bajtomil. W związku z tym spółka planuje teraz wybudować kasy na samej autostradzie.
Bajtazar przejechał autostradą i, korzystając z zamontowanego w samochodzie licznika przejechanych
bajtomil, zanotował pozycje wszystkich  wjazdów (pozycja wjazdu to jego odległość od początku autostrady).
Firma postanowiła rozmieścić
wjazdów (pozycja wjazdu to jego odległość od początku autostrady).
Firma postanowiła rozmieścić 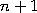 kas
równomiernie na długości autostrady, to znaczy tak, by odległość między każdymi dwiema kolejnymi kasami była taka sama.
Jednocześnie między każdymi dwiema kasami powinien być wjazd i między każdymi dwoma
wjazdami powinna być kasa.
Szczęśliwie okazało się, że przy istniejącym układzie wjazdów takie rozmieszczenie kas jest możliwe.
kas
równomiernie na długości autostrady, to znaczy tak, by odległość między każdymi dwiema kolejnymi kasami była taka sama.
Jednocześnie między każdymi dwiema kasami powinien być wjazd i między każdymi dwoma
wjazdami powinna być kasa.
Szczęśliwie okazało się, że przy istniejącym układzie wjazdów takie rozmieszczenie kas jest możliwe.
Twoim zadaniem jest obliczenie najmniejszej i
największej możliwej odległości między kasami. Mówiąc formalnie, szukamy najmniejszej i
największej wartości 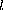 , takiej że dla pewnej pozycji
, takiej że dla pewnej pozycji 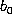 pierwszej kasy, kolejne kasy mogą zostać
umieszczone na pozycjach
pierwszej kasy, kolejne kasy mogą zostać
umieszczone na pozycjach 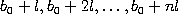 .
Dopuszczamy sytuację, w której wyznaczona w ten sposób pozycja pewnej kasy jest równa pozycji pewnego wjazdu
(wówczas kasa zostanie wybudowana tuż przed lub tuż za wjazdem).
Innymi słowy, pozycja
.
Dopuszczamy sytuację, w której wyznaczona w ten sposób pozycja pewnej kasy jest równa pozycji pewnego wjazdu
(wówczas kasa zostanie wybudowana tuż przed lub tuż za wjazdem).
Innymi słowy, pozycja 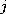 -tego wjazdu powinna zawierać się w przedziale
-tego wjazdu powinna zawierać się w przedziale 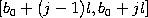 .
.
Wejście
W pierwszym wierszu wejścia znajduje się liczba całkowita  (
(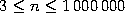 ), oznaczająca liczbę wjazdów na autostradę.
Drugi wiersz wejścia zawiera rosnący ciąg
), oznaczająca liczbę wjazdów na autostradę.
Drugi wiersz wejścia zawiera rosnący ciąg  liczb całkowitych
liczb całkowitych 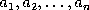 (
(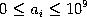 ).
Kolejne wyrazy ciągu opisują pozycje kolejnych wjazdów na autostradę w bajtomilach.
).
Kolejne wyrazy ciągu opisują pozycje kolejnych wjazdów na autostradę w bajtomilach.
Wyjście
Twój program powinien wypisać dwie liczby rzeczywiste, oznaczające
najmniejszą i największą możliwą odległość między dwiema kolejnymi kasami, w bajtomilach.
Możesz założyć, że różnica między tymi liczbami jest nie mniejsza niż 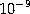 .
.
Twój wynik będzie uznany za poprawny, jeżeli znajduje się w przedziale
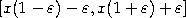 , gdzie
, gdzie  jest prawidłową
odpowiedzią, a
jest prawidłową
odpowiedzią, a 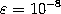 .
Tak więc tolerowany będzie zarówno błąd względny, jak i błąd bezwzględny równy
.
Tak więc tolerowany będzie zarówno błąd względny, jak i błąd bezwzględny równy  .
.
Przykład
Dla danych wejściowych:
6 2 3 4 5 6 7
poprawną odpowiedzią jest:
0.833333333333 1.250000000000
Autor zadania: Jakub Radoszewski
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English